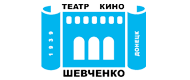
- матриця переміщення
- матриці обертання
- матриця масштабування
- комбінування перетворень
- Деякі функції для перетворення векторів
Створюючи використовують Direct3D програми, для подання перетворень ми будемо застосовувати матриці 4 × 4. Ідея полягає в наступному: ми инициализируем елементи матриці X розміром 4 × 4 таким чином, щоб вони описували необхідне перетворення. Потім ми поміщаємо координати точки або компоненти вектора в стовпці вектора-рядка v розміром 1 × 4. Результатом твори vX буде новий перетворений вектор v '. Наприклад, якщо матриця X являє переміщення на 10 одиниць уздовж осі X, і v = [2, 6, -3, 1], твір vX = v '= [12, 6, -3, 1].
Слід пояснити кілька моментів. Ми використовуємо матриці розміру 4 × 4 з тієї причини, що вони дозволяють представити всі необхідні нам перетворення. На перший погляд матриці розміром 3 × 3 здаються більш придатними для тривимірної графіки. Однак, з їх допомогою можна уявити ряд перетворень, які можуть нам знадобитися, таких як переміщення, перспективна проекція і відображення. Пам'ятайте, що ми працюємо з твором вектора на матрицю і при виконанні перетворень обмежені правилами множення матриць. Доповнення матриці до розміру 4 × 4 дозволяє нам за допомогою матриці описати більшість перетворень і при цьому твір вектора на матрицю буде визначено.
Ми згадали, що координати точки або компоненти вектора будемо зберігати в шпальтах вектора-рядка розміром 1 × 4. Але наші точки і вектори - тривимірні! Навіщо ж використовувати вектор-рядок 1 × 4? Ми повинні доповнити наші тривимірні точки / вектори до чотиривимірного вектора-рядка 1 × 4 щоб був визначений результат множення вектора на матрицю; твір вектора-рядка 1 × 3 і матриці 4 × 4 не визначене.
Так яке ж значення використовувати для четвертої компоненти, яку, до речі, ми будемо позначати w? Коли вектор-рядок 1 × 4 використовується для представлення точки, значення w дорівнюватиме 1. Це дозволяє коректно виконувати переміщення точки. Оскільки вектор не залежить від місця розташування, операція переміщення векторів не визначена і результат спроби перемістити вектор не має сенсу. Щоб запобігти переміщенню векторів ми, поміщаючи компоненти вектора в вектор-рядок 1 × 4, присвоюємо компоненті w значення 0. Наприклад, точка p = (p 1, p 2, p 3), вміщена в вектор-рядок 1 × 4 буде виглядати як [p 1, p 2, p 3, 1], а вектор v = (v 1, v 2, v 3), поміщений в вектор-рядок 1 × 4 буде виглядати як [v 1, v 2, v 3, 0 ].
ПРИМІТКА
Ми встановлюємо w = 1 щоб коректно здійснювалося переміщення точок. Ми встановлюємо w = 0, щоб запобігти переміщенню векторів. Це стане ясніше, коли ми розглянемо реальну матрицю перенесення.
ПРИМІТКА
Доповнений чотиривимірний вектор називається однорідним вектором (homogenous vector) і, оскільки однорідний вектор може описувати і точки і вектори, ми будемо використовувати термін «вектор», маючи на увазі, що він може ставитися як до точки, так і до вектора.
Іноді в результаті перетворень компонента w вектора буде змінюватися таким чином, що w ≠ 0 і w ≠ 1. Погляньте на наступний приклад:
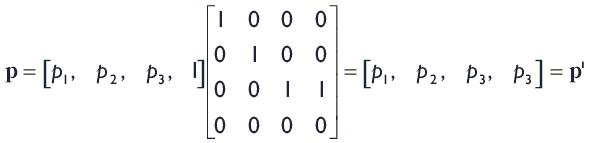
для p 3 ≠ 0 і p 3 ≠ 1.
Зверніть увагу, що w = p 3. Коли w ≠ 0 і w ≠ 1, ми говоримо, що у нас є вектор в однорідному просторі (homogeneous space), на противагу векторах в тривимірному просторі. Ми можемо відобразити вектор в однорідному просторі назад на тривимірний простір, розділивши кожну компоненту вектора на значення компоненти w. Наприклад, для відображення вектора (x, y, z, w) в однорідному просторі в тривимірний вектор x, виконаємо наступні операції:
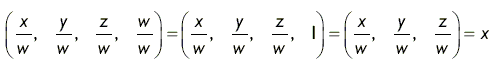
Перехід до однорідного простору і зворотне відображення векторів в тривимірний простір використовуються в програмуванні тривимірної графіки для виконання перспективної проекції.
ПРИМІТКА
Коли ми записуємо точку (x, y, z) у вигляді (x, y, z, 1) ми фактично описуємо наше тривимірний простір як площину в чотиривимірному просторі, а саме чотиривимірну площину w = 1. (Зверніть увагу, що площина в чотиривимірному просторі є тривимірним простором, точно так само як площину в тривимірному просторі є двовимірним простором.) Таким чином, привласнюючи w яке-небудь інше значення, ми подорожуємо з полскості w = 1. Щоб повернутися на цю площину, яка відповідає нашому тривимірному про транству, ми виконуємо зворотний проекцію шляхом ділення кожної компоненти на w.
матриця переміщення
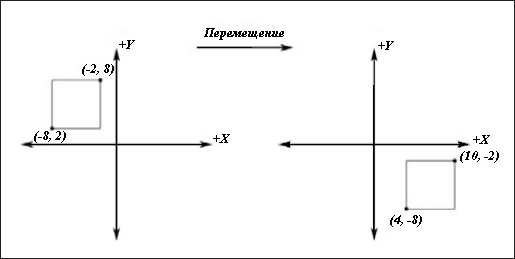
Мал. 8. Переміщення на 12 одиниць по осі X і на -10 одиниць по осі Y
Ми можемо перемістити вектор (x, y, z, 1) на px одиниць по осі Х, py одиниць по осі Y і pz одиниць по осі Z помноживши його на наступну матрицю:
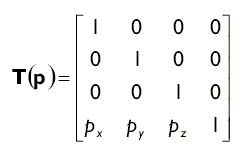
Для створення матриці переміщення в бібліотеці D3DX використовується наступна функція:
D3DXMATRIX * D3DXMatrixTranslation (D3DXMATRIX * pOut, // Результат FLOAT x, // Кількість одиниць для переміщення по осі X FLOAT y, // Кількість одиниць для переміщення по осі Y FLOAT z // Кількість одиниць для переміщення по осі Z);
ВПРАВА
Нехай T (p) - це матриця, що представляє перетворення переміщення і нехай v = [v 1, v 2, v 3, 0] - це довільний вектор. Перевірте, що v T (p) = v (тобто, що якщо w = 0, перетворення переміщення не впливає на вектор).
Інверсія матриці переміщення виходить шляхом простої зміни знака компонент вектора переміщення p.
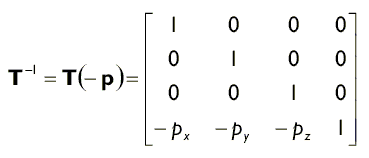
матриці обертання

Мал. 9. Поворот на 30 градусів проти годинникової стрілки навколо осі Z
Використовуючи наведені нижче матриці ми можемо повернути вектор на φ радіан навколо осей X, Y або Z. Зверніть увагу, що якщо дивитися вздовж осі обертання у напрямку до початку координат, то кути вимірюються за годинниковою стрілкою.
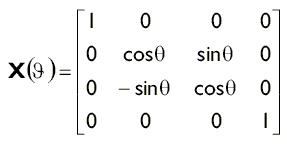
Для створення матриці обертання навколо осі X в бібліотеці D3DX використовується наступна функція:
D3DXMATRIX * D3DXMatrixRotationX (D3DXMATRIX * pOut, // Результат FLOAT Angle // Кут повороту в радіанах); 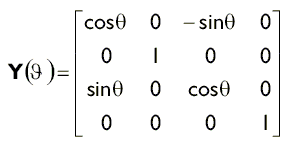
Для створення матриці обертання навколо осі Y в бібліотеці D3DX використовується наступна функція:
D3DXMATRIX * D3DXMatrixRotationY (D3DXMATRIX * pOut, // Результат FLOAT Angle // Кут повороту в радіанах); 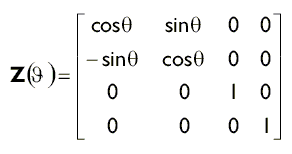
Для створення матриці обертання навколо осі Z в бібліотеці D3DX використовується наступна функція:
D3DXMATRIX * D3DXMatrixRotationZ (D3DXMATRIX * pOut, // Результат FLOAT Angle // Кут повороту в радіанах);
Інверсією матриці обертання R є результат транспонування цієї матриці: R T = R-1. Такі матриці називаються ортогональними.
матриця масштабування
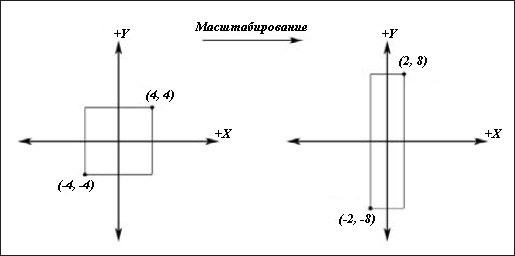
Мал. 10. Масштабування з коефіцієнтом 1/2 по осі X і коефіцієнтом 2 по осі Y
Ми можемо масштабувати вектор з коефіцієнтом qx по осі Х, коефіцієнтом qy по осі Y і коефіцієнтом qz по осі Z, помноживши його на наступну матрицю:
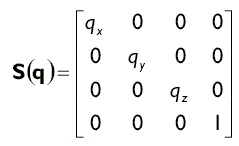
Для створення матриці масштабування в бібліотеці D3DX використовується наступна функція:
D3DXMATRIX * D3DXMatrixScaling (D3DXMATRIX * pOut, // Результат FLOAT sx, // Коефіцієнт масштабування по осі X FLOAT sy, // Коефіцієнт масштабування по осі Y FLOAT sz // Коефіцієнт масштабування по осі Z);
Щоб інвертувати матрицю масштабування треба взяти зворотну дріб для кожного коефіцієнта масштабування:
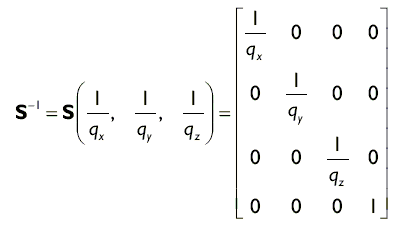
комбінування перетворень
Часто ми будемо застосовувати до векторів цілу послідовність перетворень. Наприклад, ми можемо масштабувати вектор, потім повернути його і потім перемістити в потрібну позицію.
Як приклад ми розглянемо вектор p = [5, 0, 0, 1], який масштабується по всіх осях з коефіцієнтом 1/5, потім повернемо його на π / 4 радіан навколо осі Y і, нарешті, перемістимо на 1 одиницю по осі X, 2 одиниці по осі Y і -3 одиниці по осі Z.
Зверніть увагу, що ми повинні виконати масштабування, поворот навколо осі Y і переміщення. Ми инициализируем наші матриці перетворень S, R y, T для масштабування, повороту і переміщення відповідно, наступним чином:
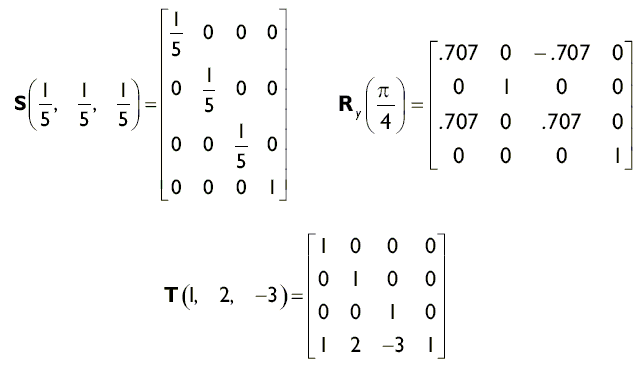
Застосувавши послідовність перетворень в заданому порядку - масштабування, обертання, переміщення - отримаємо:
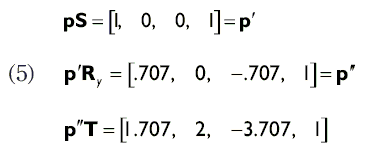
Ключовою перевагою використання матриць є можливість використання множення матриць для комбінування декількох перетворень в одній матриці. Повернемося до прикладу, розглянутого на початку даного розділу. Давайте за допомогою множення матриць скомбініруем все три матриці перетворень в одну, яка буде представляти всі три перетворення відразу. Зверніть увагу, що порядок, в якому ми множимо матриці повинен відповідати порядку застосування окремих перетворень.
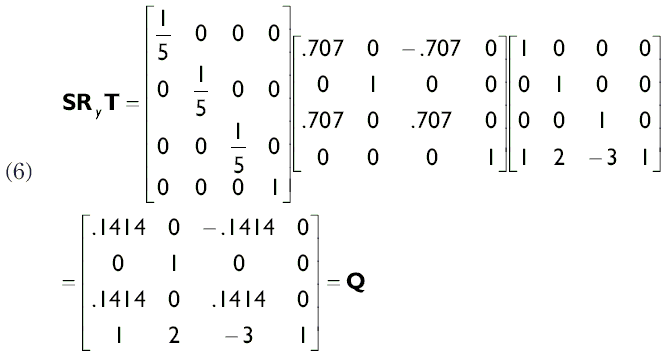
В результаті отримуємо pQ = [1.707, 2, -3.707, 1].
Можливість комбінувати перетворення значно збільшує продуктивність. Уявіть, що вам необхідно застосувати одну і ту ж послідовність перетворень масштабування, обертання і переміщення до великого набору векторів (це звичайне завдання в тривимірній комп'ютерній графіці). Замість того, щоб застосовувати до кожного вектору послідовність перетворень, як ми робили це у формулі (5), можна скомбінувати все три перетворення в одній матриці, як ми робили це у формулі (6). Після цього залишається тільки помножити кожен вектор на єдину матрицю, що містить комбінацію всіх трьох перетворень. Завдяки цьому кількість виконуваних операцій множення вектора на матрицю значно скорочується.
Деякі функції для перетворення векторів
Бібліотека D3DX надає дві функції для перетворення точок та векторів відповідно. Функція D3DXVec3TransformCoord використовується для перетворення точок та передбачає, що четверта компонента вектора дорівнює 1. Функція D3DXVec3TransformNormal використовується для перетворення векторів і передбачає, що четверта компонента вектора дорівнює 0.
D3DXVECTOR3 * D3DXVec3TransformCoord (D3DXVECTOR3 * pOut, // Результат CONST D3DXVECTOR3 * pV, // Перетворювані точка CONST D3DXMATRIX * pM // Матриця перетворення); D3DXMATRIX T (...); // ініціалізація матриці перетворень D3DXVECTOR3 p (...); // ініціалізація точки D3DXVec3TransformCoord (& p, & p, & T); // перетворення точки D3DXVECTOR3 * D3DXVec3TransformNormal (D3DXVECTOR3 * pOut, // Результат CONST D3DXVECTOR3 * pV, // Перетворювані вектор CONST D3DXMATRIX * pM // Матриця перетворення); D3DXMATRIX T (...); // ініціалізація матриці перетворень D3DXVECTOR3 v (...); // ініціалізація вектора D3DXVec3TransformNormal (& v, & v, & T); // перетворення вектора
ПРИМІТКА
Бібліотека D3DX також надає функції D3DXVec3TransformCoordArray і D3DXVec3TransformNormalArray для перетворення масиву точок і масиву векторів відповідно.
Сайт управляється системою uCoz